Comprendre la « règle de 16 »

Les négociateurs d’options professionnels sont vraiment doués pour ce qui est de la division et de la multiplication par 16. Cela peut paraître étrange, mais c’est une compétence essentielle pour quiconque souhaite maîtriser la terminologie spécifique aux marchés des options. Peu importe l’usage que vous faites des options, la « règle de 16 » est essentielle pour analyser la volatilité, en particulier lorsqu’il s’agit des options à court terme.
Que vous utilisiez les options à des fins de négociation, de couverture ou d’investissement, il importe de vous familiariser avec les mesures de volatilité courantes. La volatilité est à la base de l’établissement du prix des options. Elle repose sur le concept statistique de l’écart-type, une mesure de la dispersion des rendements d’un titre par rapport à sa moyenne. Chaque jour de bourse, les cours fluctuent à la hausse comme à la baisse. Plus les fluctuations du cours d’un titre sont fortes, plus l’écart-type de ce dernier est élevé. La dispersion des variations quotidiennes des cours, mesurée en pourcentage sur une période donnée, est à la base du concept de la volatilité.
La volatilité implicite est une valeur statistique couramment citée et observée. De nombreux fournisseurs de services et maisons de courtage l’affichent aux côtés du prix des options sur leurs plateformes (comme celle d’Interactive Brokers). Deux caractéristiques de la volatilité implicite sont souvent mal comprises des investisseurs. D’abord, il s’agit d’une valeur dérivée. Elle est la variable résiduelle de tout modèle d’évaluation des options après la prise en compte des autres variables que sont le cours du titre sous-jacent, le prix de levée de l’option, le temps restant à courir avant l’échéance de l’option, les dividendes attendus du titre sous-jacent avant l’échéance de l’option et les taux d’intérêt en vigueur pendant la durée de vie de l’option. Ensuite, la volatilité implicite est généralement exprimée sur une base annualisée. C’est là que la règle de 16 entre en jeu.
Tableau 1 : Données concernant le prix de l’option de vente sur le FNB XIU au prix de levée de 20 $ échéant le 15 mai 2020, tirées du rapport de fin de journée de la Bourse de Montréal du 14 avril 2020
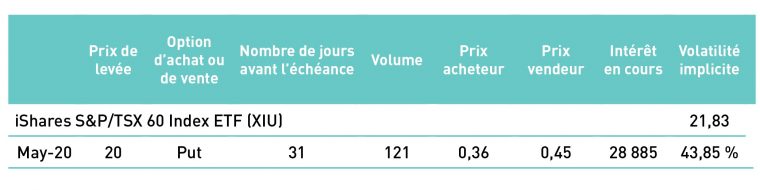
Source : Bourse de Montréal
Dans l’exemple qui précède, il est question de l’option de vente sur le fonds négocié en bourse (FNB) XIU ayant un prix de levée de 20 $ et venant à échéance le 15 mai 2020. Sur la base des données qui figurent au tableau, à savoir un cours de clôture de 21,83 $ du FNB XIU, une période de 31 jours restant avant l’échéance de l’option et un point médian de 0,405 $ ([0,36 $ + 0,45 $] ÷ 2) de l’écart acheteur-vendeur de l’option au prix de levée choisi, on calcule une volatilité implicite de 43,85 %. Ce résultat indique que le marché s’attend à une variation annualisée d’environ 44 % du cours du FNB XIU pendant la période des 31 prochains jours. Malheureusement, une valeur annualisée est foncièrement dénuée de sens pour le détenteur d’une option venant à échéance dans environ un mois. La règle de 16 est ce qui nous permet de replacer cette volatilité implicite de 43,85 % dans un contexte significatif.
Il existe une méthode toute simple pour convertir la volatilité annualisée en volatilité quotidienne. Il suffit de diviser le résultat annualisé par la racine carrée du nombre de jours ouvrables que compte normalement une année, soit un peu moins de 256 jours. Or, il se trouve que la racine carrée de 256 est 16, d’où la règle de 16. En reprenant l’exemple qui précède, on obtient le résultat suivant :
43,85 % ÷ 16 = 2,74 %
Cela signifie que les participants du marché des options s’attendent à ce que les fluctuations moyennes du cours du FNB XIU, à la hausse comme à la baisse, soient d’environ 2,74 % par jour pendant la durée de vie de l’option. Les parts du FNB XIU se négociant à 21,83 $, le pourcentage calculé représente des fluctuations d’environ 0,60 $. Il est nettement plus facile pour un investisseur d’imaginer que le cours du FNB XIU fluctuera en moyenne de 0,60 $ par jour, à la hausse ou à la baisse, au cours des prochaines semaines. Les investisseurs qui sont d’avis que le marché sous-estime les fluctuations quotidiennes à venir du cours du FNB devraient envisager d’acheter des options au niveau actuel de volatilité. Ceux qui sont de l’opinion contraire devraient plutôt s’abstenir d’acheter des options dans ces conditions; ils devraient même envisager d’en vendre.
La règle de 16 s’avère particulièrement utile tout juste avant la publication des résultats financiers des sociétés. Voici d’autres données tirées du même rapport de fin de journée de la Bourse de Montréal :
Tableau 2 : Données concernant le prix de l’option d’achat sur les actions TECK au prix de levée de 12 $ échéant le 24 avril 2020, tirées du rapport de fin de journée de la Bourse de Montréal du 14 avril 2020
| Prix de levée | Option d’achat ou de vente | Nombre de jours avant l’échéance | Volume | Prix acheteur | Prix vendeur | Intérêt en cours | Volatilité implicite | |
| Teck Resources Limited, Cl. B (TECK) | 12,32 | |||||||
| Avril 2020 | 12 | Option d’achat | 10 | 10 | 0,68 | 0,75 | 185 | 67,67 % |
Source : Bourse de Montréal
Les données qui précèdent concernent l’option d’achat sur les actions TECK ayant un prix de levée de 12 $ et venant à échéance le 24 avril 2020. La société Teck Resources doit annoncer ses résultats financiers le 23 avril, soit un jour avant l’échéance de cette option. En appliquant la méthode de calcul décrite précédemment, on peut convertir la volatilité annualisée de 67,67 % en une volatilité quotidienne de 4,23 %, laquelle représente des fluctuations quotidiennes moyennes du cours des actions d’environ 0,52 $. Comme les cours des actions connaissent souvent une volatilité accrue lors de la séance de négociation qui suit la publication des résultats financiers correspondants, il peut être beaucoup plus facile pour les négociateurs d’évaluer si les fluctuations du cours des actions de Teck que prévoit le marché sont raisonnables.
À ce stade, vous vous demandez peut-être pourquoi les marchés persistent à exprimer la volatilité implicite des options sur une base annualisée, et ce, même si cela est nettement moins utile pour les investisseurs. Très franchement, c’est une coutume archaïque des intervenants du marché. Le modèle de Black et Scholes, premier mécanisme d’évaluation des prix des options à avoir été largement adopté par les intervenants du marché, utilise la volatilité annualisée. En fait, il implique expressément la prise en compte des fluctuations quotidiennes des prix et leur conversion en une valeur annualisée. Avant l’émergence du modèle de Black et Scholes, les options constituaient un instrument de placement mal compris des investisseurs. Elles n’étaient pas un élément fondamental de l’univers du placement comme elles le sont de nos jours. Le modèle de Black et Scholes ayant été élaboré sur la base d’une mesure annualisée de la volatilité, il en fut de même des marchés des options qui se sont développés dans son sillage. Et cette pratique persiste encore aujourd’hui à l’échelle du secteur.
J’espère sincèrement que le présent article aura contribué à démystifier la terminologie propre au concept de la volatilité pour bon nombre d’entre vous et qu’il vous aidera à mieux comprendre comment interpréter cette valeur obscure pour l’appliquer à des situations bien réelles. À l’approche d’une nouvelle saison de publication de résultats financiers trimestriels – laquelle est susceptible d’accroître le degré d’incertitude qui pèse sur les marchés –, une bonne compréhension de la règle de 16 devrait vous permettre de mieux évaluer les perspectives du marché des options quant à l’évolution des cours des titres à la suite de la publication des résultats financiers des sociétés.
L’auteur est un cadre dirigeant d’une société affiliée à Interactive Brokers Canada Inc. (« IBC »), un participant agréé de Bourse de Montréal Inc. (la « MX ») et un membre compensateur de la Corporation canadienne de compensation de produits dérivés (la « CDCC »). Rien dans le présent article ne doit être considéré comme une recommandation de placement ou de négociation émise par IBC ou l’une de ses sociétés affiliées. La négociation d’options est une activité hautement spéculative qui comporte un degré élevé de risque. Avant de négocier des options inscrites à la MX et émises par la CDCC, il est recommandé aux investisseurs de lire et de bien comprendre le document d’information de la CDCC intitulé « The Characteristics and Risks of Listed Canadian Options » (en anglais).
Chief Strategist, Interactive Brokers
Steve Sosnick est stratège en chef d’Interactive Brokers. Il est également négociateur en chef de Timber Hill, division de négociation de la société, et membre du Groupe Interactive Brokers, société de portefeuille de l’entreprise. Steve a occupé de nombreux postes au sein de l’organisation depuis son entrée en fonction comme gestionnaire du risque boursier et mainteneur de marché d’options à Timber Hill en 1995. Il a mené l’établissement de la société au Canada en 1998 et depuis, il dirige Timber Hill Canada. Il a consacré une bonne partie de sa carrière à la mise au point et à la mise en œuvre de stratégies de négociation électronique et algorithmique pour les actions et les options avant d’assumer un rôle plus stratégique au sein de l’organisation, soit celui de stratège en chef des options, et plus tard, celui de stratège en chef. Steve a signé plusieurs chroniques publiées dans l’hebdomadaire Barron’s et il est régulièrement invité par les réseaux Bloomberg TV et Bloomberg Radio ainsi que par Yahoo Finance. Il a siégé au conseil d’administration de divers marchés boursiers. Il a aussi été membre des conseils de CBSX, de NSE et de ISE-SE. Au Canada, il est membre du Groupe des usagers de la Division de la réglementation de la Bourse de Montréal et du Comité de produits dérivés de l’Association canadienne du commerce des valeurs mobilières. Avant de se joindre à Interactive Brokers, Steve a occupé le poste de négociateur principal chez Morgan Stanley, Lehman Brothers et Salomon Brothers et a suivi au sein de cette dernière société le réputé programme de formation. Steve est titulaire d’une maîtrise en finance et d’un baccalauréat en sciences économiques de The Wharton School de l’université de la Pennsylvanie.
Les informations contenues sur ce site web, incluant notamment les données financières et économiques, les cours boursiers ainsi que toute analyse et toute interprétation de ces informations, sont fournies à titre informatif seulement et ne peuvent être interprétées, dans aucun territoire, comme étant un conseil ou une recommandation relativement à l’achat ou la vente d’instruments dérivés, de titres sous-jacents ou d’autres instruments financiers, ou comme étant un avis de nature juridique, comptable, fiscal, financier ou de placement. Bourse de Montréal Inc. vous recommande de consulter vos propres conseillers selon vos besoins avant de prendre toute décision quant à vos objectifs d’investissement, votre situation financière et vos besoins spécifiques.
Toute mention figurant sur ce site web relative aux caractéristiques, aux règles et aux obligations concernant un produit est faite sous réserve des règles, politiques et procédures de Bourse de Montréal Inc. et de sa chambre de compensation, la Corporation canadienne de compensation de produits dérivés, et celles-ci auront préséance sur le contenu de ce site web. Bien que les documents publiés sur ce site web aient été conçus, préparés et rédigés avec soin, Bourse de Montréal Inc. et ses sociétés affiliées ne garantissent pas l’exactitude ou l’exhaustivité de l’information qu’ils renferment et se réservent le droit de modifier ou de réviser, à tout moment et sans préavis, la teneur de ces documents. Bourse de Montréal Inc., ses sociétés affiliées, ses administrateurs, ses dirigeants, ses employés et ses mandataires ne pourront être tenus responsables des dommages, des pertes ou des frais découlant des erreurs ou omissions de ce site web, à tout moment, ou de l’utilisation des renseignements y figurant et des décisions prises sur la base de ceux-ci.
BAXMD, CADCMD, CGBMD, CGFMD, CGZMD, LGBMD, MXMD, OBXMD, OGBMD, OIS-MXMD, ONXMD, SCFMD, SXAMD, SXBMD, SXFMD, SXHMD, SXMMD, SXOMD, SXYMD, et USXMD sont des marques déposées de la Bourse. OBWMC, OBYMC, OBZMC, SXKMC, SXJMC, SXUMC, SXVMC, Bourse de Montréal et le logo de la Bourse de Montréal sont des marques de commerce de la Bourse. Toutes les autres marques de commerce utilisées appartiennent à leurs propriétaires respectifs.
© 2024 Bourse de Montréal Inc. Tous droits réservés.
